Linear regression is a statistical model for predicting the value of a single dependent (criterion) variable from one or more independent (predictor) variables. Researchers use it to explain or predict a target variable, whether working with a single predictor (simple regression) or several predictors that jointly contribute to the prediction (multiple regression). SmartPLS lets you estimate single and multiple regression models directly in the software and provides comprehensive result reports, including regression coefficients, diagnostic plots, and settings for evaluating the outcomes.

As described by Hair, Black, Babin, and Anderson (2018), multiple regression analysis is a statistical technique that can be used to analyze the relationship between a single dependent (criterion) variable and several independent (predictor) variables (see also Backhaus, Erichson, Gensler, Weiber, & Weiber, 2021; Sarstedt & Mooi, 2019). The objective of multiple regression analysis is to use the independent variables whose values are known to predict the single dependent value selected by the researcher. Each independent variable is weighted by the regression analysis procedure to ensure maximal prediction from the set of independent variables. The weights denote the relative contribution of the independent variables to the overall prediction and facilitate interpretation as to the influence of each variable in making the prediction, although correlation among the independent variables complicates the interpretative process. Thus, it can equally achieve the objectives of prediction or explanation.

The set of weighted independent variables forms the regression variate, a linear combination of the independent variables that best predicts the dependent variable. The regression variate, also referred to as the regression equation or regression model, is the most widely known example of a variate among the multivariate techniques.

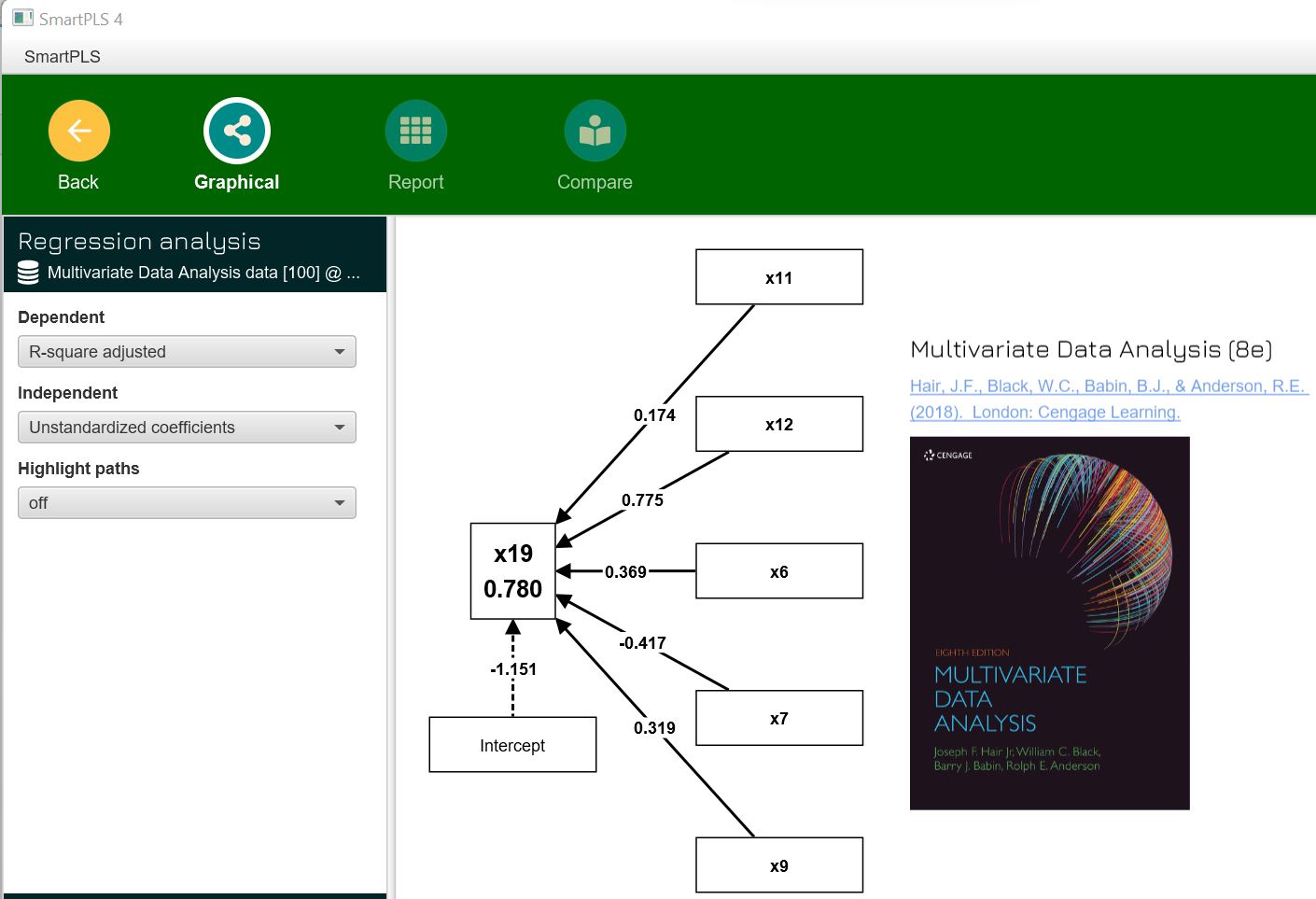
The following figure illustrates a multiple regression model established in SmartPLS. The software enables the estimation of single and multiple regression models and reports the corresponding regression coefficients in both unstandardized and standardized form. When specified, an intercept is included in the estimation, as shown in the figure. To estimate a regression model without an intercept in SmartPLS, the intercept must be removed from the graphical specification of the regression model (i.e., select and delete the intercept).

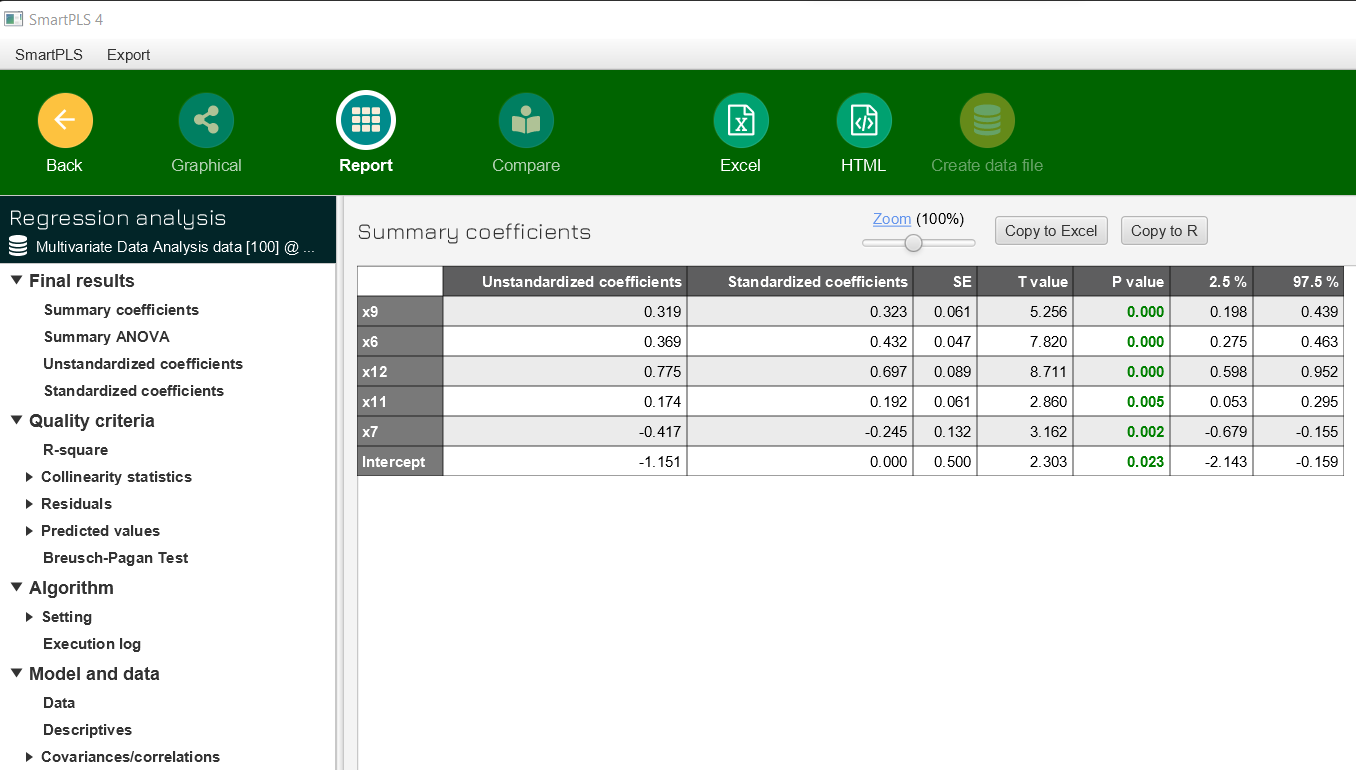
The SmartPLS results report for the regression analysis provides all the results to perform a systematic model evaluation according to generally accepted criteria. The following figure provides a results report example.

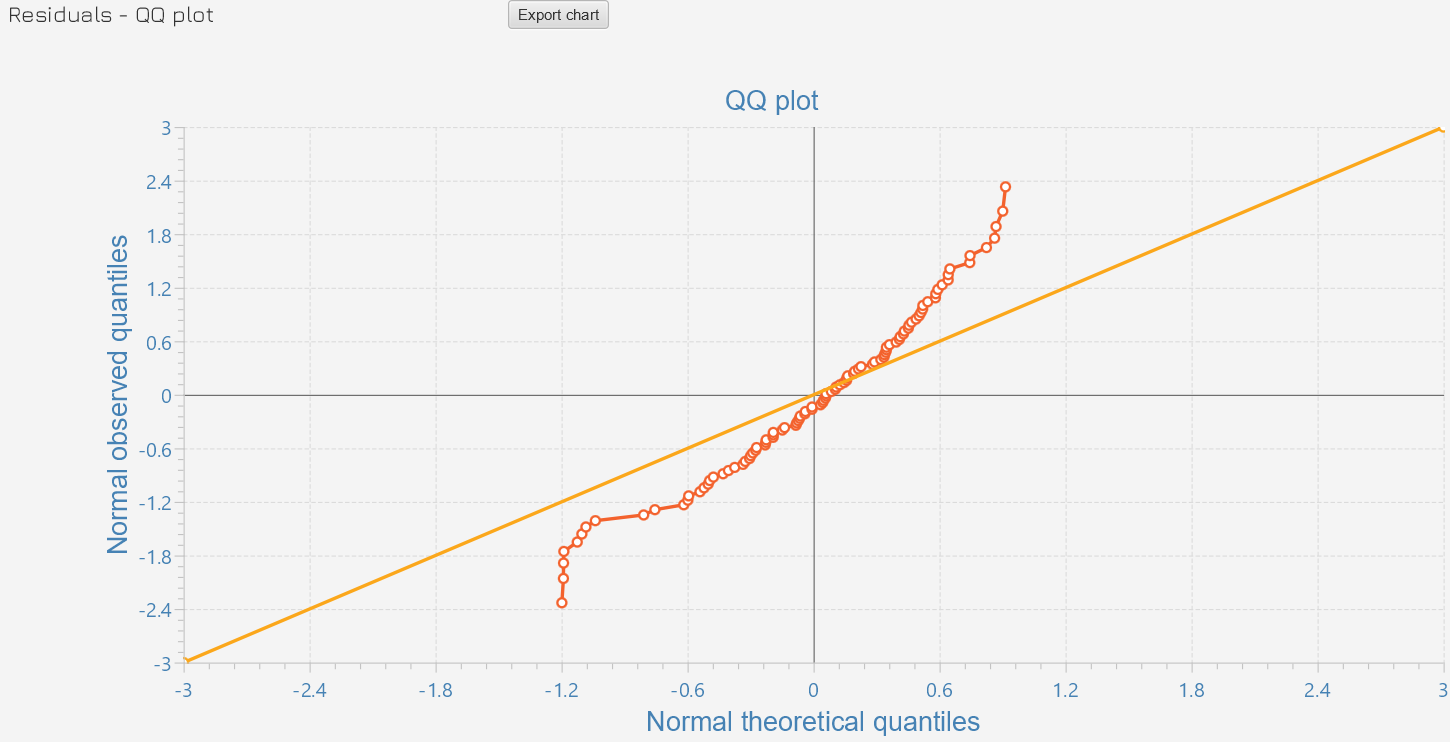
In addition, the SmartPLS report contains several graphical representations of regression model results. For example, the following figure displays the QQ-plot provided by SmartPLS.

For SmartPLS, we provide sample projects for running regression analysis, including the Gaussian copula approach, logistic regression, and necessary condition analysis. Simply download, import, and run these examples in SmartPLS.

Specifies if a one-sided or two-sided significance test is conducted.

Specifies the significance level of the test statistic.

As an alternative to the normal standard errors (HC0), users can select the heteroscedasticity consistent (HC) standard errors HC3 or HC4 in SmartPLS.

Linear regression predicts the value of a single dependent variable from one or more independent variables. It can serve either a prediction objective or an explanation objective: the weights assigned to the independent variables show their relative contribution to the prediction and support interpreting each variable's influence, keeping in mind that correlation among the independent variables complicates this interpretation.

The regression variate is the linear combination of weighted independent variables that best predicts the dependent variable. It is also referred to as the regression equation or regression model and is the most widely known example of a variate among multivariate techniques.

Yes. By default, SmartPLS includes an intercept when a regression model is specified graphically. To estimate the model without an intercept, remove the intercept from the graphical model specification by selecting and deleting it.

Normal standard errors (HC0) are the default. If you suspect heteroscedasticity in your data, the heteroscedasticity-consistent alternatives HC3 or HC4 provide more robust standard errors: HC3 approximates a jackknife estimator by dividing squared residuals by the square of 1-h, while HC4 divides squared residuals by 1-h raised to a power that varies according to h, N, and p (with an upper limit of 4).

SmartPLS lets you specify a one-sided or two-sided significance test and the significance level of the test statistic. For nonparametric significance testing based on resampling, see regression bootstrapping.

Not with the standard regression method described here, which assumes a continuous dependent variable. For a binary (dichotomous) dependent variable, use logistic regression instead.